机器学习笔记-吴恩达的机器学习课(第二周)
一、多元线性回归(Multivariate Linear Regression)
矩阵乘法:解决多项式线性回归的问题
回归的表达式可以用一个相乘的矩阵来简单地表示:

对应的梯度下降算法也就变成了:

对应的计算技巧:
1)特征缩放(Feature Scaling)
比如,有两个参数,一个取值范围在(0,2000)之间,一个在(1,5)之间,我们可以将它们全部归一化地映射到(0,1)之间,这样算法会更快地收敛。
我们通常将特征值放到(-1,1)之间,当然,这个区间是可以自己选择的,一般来说,在[-3,3]之间都是可以的。
归一化,并不仅仅是上面的映射,可能会更多一点,操作,比如为了将[30,50]之间的一系列数字归一化,可以先计算这些数字的平均数,比如38,然后用(x-38)/20的方式将其归一化。
它们的目的是使梯度下度的速度变的更快,让梯度下降收敛所需的循环次数更少。
2)学习率(Learning Rate)
简单理解为每一步迭代时步子的大小,对于一个图形来说,学习率越小肯定是越好,但是,小的话,迭代的次数也就越多。因为相当于步子迈的小了。为了提高效率,减少迭代次数,我们考虑将α的值调大一点,但是大了的话,又有另外一个问题,就是有可能会迈过谷底,到另一边去了,这样就会错过最优解。
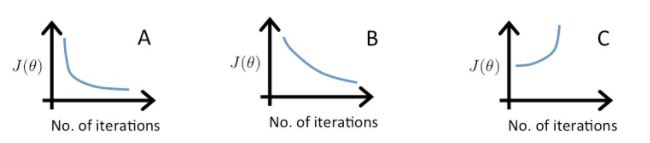
如上图,C中,代价函数一直在增长,这样肯定是不对的,明显α值太大了。A和B都是正常的,但B表现的更好。表现不好的图,肯定是α值大了,只要将这个值调到图形表现最好的最大值,就OK了。
当然,选择一个恰当的α值比较困难,但可以试试……,0.003,0.03,0.3,3……
3)创造新的特征
有些特征是可以合并,或者计算出一个新的特征的,比如,有长和宽,完全可以长乘以宽得出面积,把面积作为一个特征来计算。
4)多项式回归转线性的技巧:
对于一个点的集合,要拟合它,可以有多个不同的模型可选择,比如一根直线,也可以是一个一元二次方程式,也可以是一个一元三次方程,主要是这些点都只是一个曲线的一部分,而选择哪一个模型,则基于一些个人的判断,比如对趋势的预期等。
这里举了一个例子,就是如果我们对一个特定的集合进行拟合,比如下图的房屋面积和房价的图例
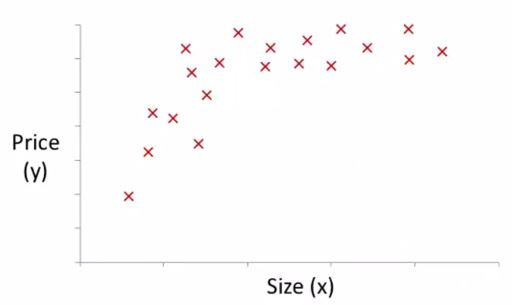
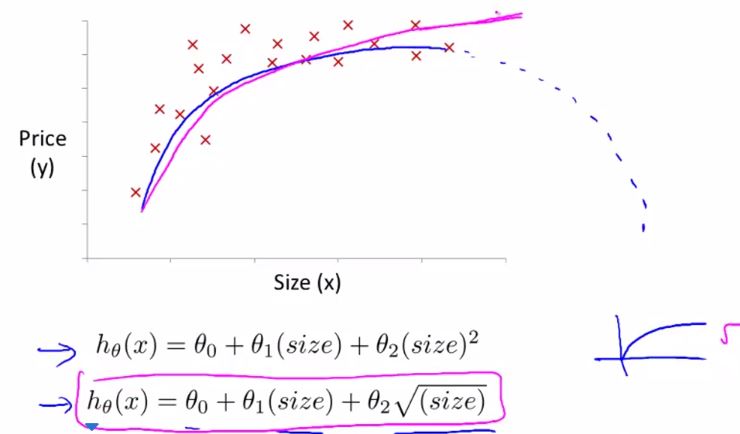
因为用二次函数的话,图形会下降,假如我们认为房价并不会下降,所以决定用三次函数,
![]()
来拟合,我们可以通过x1的平方和x1的立方作为两个新的特征值,将其转变成一个多元线性回归来计算,这时,归一化就显的重要了,因为如果x1的值的范围是[1,1000],x2的范围就是[1,1000*1000],x3的范围就变成了[1,1000*1000*1000],按我们原来说的,要想梯度运算有效率,就得把它们归一化后再进行计算。
但我们还有另外一个选择,这个技巧依然是在特征值上作文章:
二、计算参数分析(Computing Parameters Analytically)
正规方程算法:如果对于一个代价函数的U型图来说,当作一个y=a+bx*x的一元二次函数,其实是可以直接计算出这个最小值的,只要找出导数为0的点即可,那么对于一系列的离散点,只需要对每个点求偏导数为0时的值,找最小值即可,但是在实际中,如果对每个点都求偏导数,计算量会很大,所以这里需要一些计算技巧和方法。
正规方程算法的公式是:
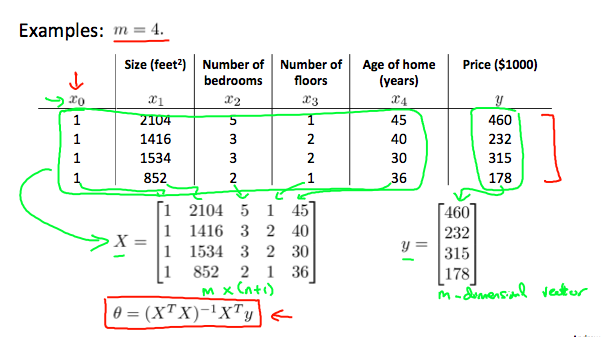
这里并不需要对特征值 进行特征缩放。
下面是梯度下降算法和正规方程法的优缺点对比
| Gradient Descent | Normal Equation |
|---|---|
| 需要选择工作速率alpha | 不需要选择alpha |
| 需要多次迭代 | 不需要迭代 |
| 计算复杂度低O (kn2) | 计算复杂度高O (n3), 需要计算转置矩阵与矩阵的乘法 |
| 在维度n大时工作的很好 | 如果维度n很大,工作的的很慢 |
一个简单的选择就是n>1万时,选择梯度下降算法。
对于正规方程公式中 θ=inv(X’X ) X’y来说,如果X’X矩不可逆怎么办?
首先,这种情况很少见,如果出现了,我们可以
1)看看有没有多余的特征,对一些多余的特征进行合并或删减
2)如果特征数量太多,用较少的特征来反映尽可能多的内容
3)如果在Octave中,用伪逆函数pinv()来运算。而不是用inv()来计算。
