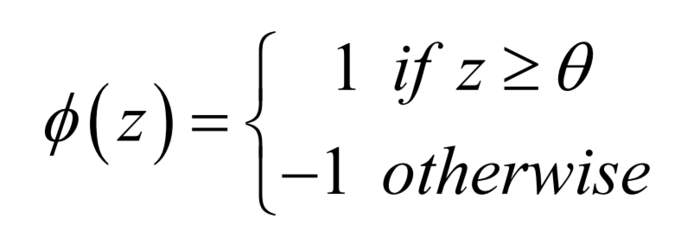1）Rossenblatt感知器

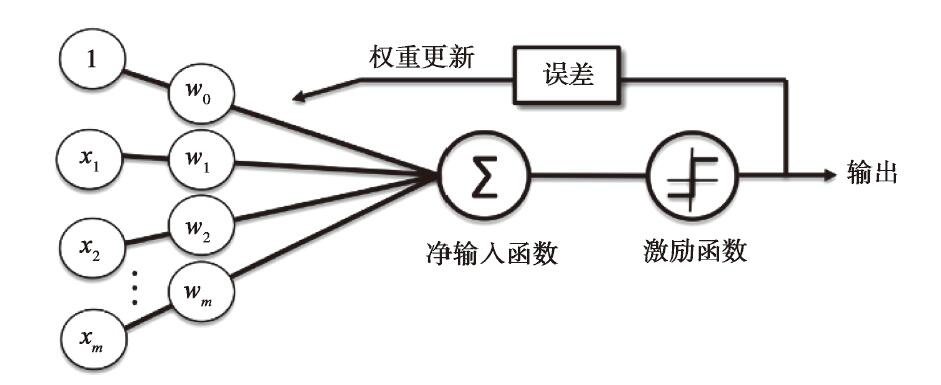
对于每一行数据，有m个参数（变量）和一个输出（标签），先对每个参数x定义一个初始的权重w

净输入函数定义为：z＝w₀x₀₊w₁x₁＋…＋w_mx_m。注意，这里增加了一个W₀X_0。

然后对这个z值，通过激励函数来判断，

如果计算出的值和标签值相同，都是1或者-1，则w不做变化，进入下一轮，如果不同，则向某个方向调整w的值，进入下一轮的回测比较。

查看python实现的例子,能看到在更新权重时，用到了一个小技巧，使得代码非常简洁

for xi, target in zip(X, y): #zip将两个对象打包成一个元组，比如这里，X是一个100x2的阵列，100行，每行2列，而y是100行，每行1列，打包后，相当于[(x1,x2),y1]
    update = self.eta*(target - self.predict(xi))
    self.w_[1:] += update*xi #很显然，如果上一行括号里两个值相等，相当于实际值和预测量相同，这时update=0,则w_的值不会变化
    self.w_[0] += update
    errors += int(update != 0.0)
self.errors_.append(errors)

上面X就是n个二元组，比如[14.1,22],[11.4,31.3]……，而y则是一个长度为n的数列[-1,1,……]，相当于是每一个X对应的标签。

而净输入函数net_input非常简单

def net_input(self, X):
    """Calculate net input"""
    return np.dot(X, self.w_[1:]) + self.w_[0]

激励函数，这里是预测函数

def predict(self, X):
    """Return class label after unit step"""
    return np.where(self.net_input(X) >= 0.0, 1, -1)

这里有一个问题是，为什么要加一个W₀。

增加的第一个权重值，主要是用来作为阀值，当设定W₀=0时 ，相当于阀值为0， 当这个激励函数>=0.0时，就是1，否则就是-1。

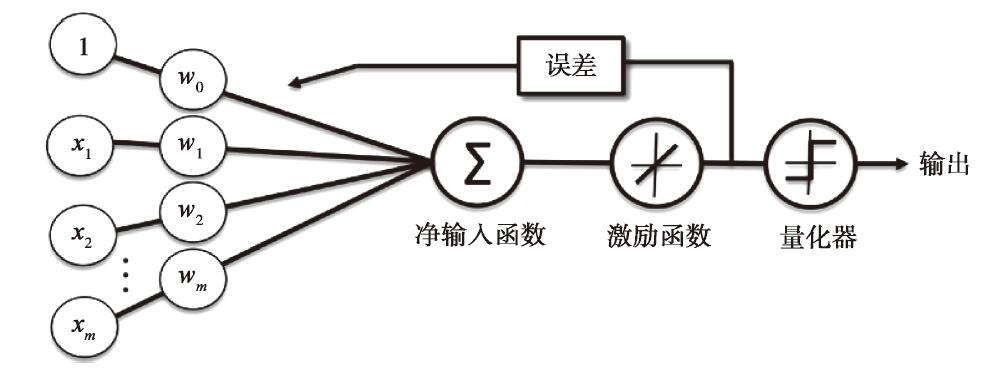
2）自适应线性神经网络（Adaptive Linear Neuron,ADaline）

可以通过查看Python实现的算法来了解此感知器的技术细节。

可以看到，主要区别在于Fit函数。

def fit(self, X, y):
    self.w_ = np.zeros(1 + X.shape[1])
    self.costs_ = []

    for i in range(self.n_iter):
        output = self.net_input(X)
        errors = (y - output)
        self.w_[1:] += self.eta * X.T.dot(errors)
        self.w_[0] += self.eta * errors.sum()
        cost = (errors ** 2).sum() / 2.0
        self.costs_.append(cost)
    return self

Rosenblatt的算法中Fit函数里，每一轮迭代中，对每一个样本做一次权重更新，而这里的算法是用代价函数的方式来进行。代价函数从概念上比较容易理解，它是一个凸函数，所以可以理解成在每次迭代时找最小值，这时，如果学习速率过大，相当于跨度过大，有可能会跳过最优解，而学习速度小，则需要更多的迭代次数，这就需要根据经验来调整参数。但是从上面的算法，看起来还是比较生涩难懂的。

因为它需要在每轮迭代中对全局数据进行运算，如果数据量大了的话，会存在成本问题， 这时可以考虑一种替代的优化算法：随机梯度下降。

3）逻辑回归算法

对于上面的Adaline算法，修改三点：

• 将代价函数由平方误差改为对数似然函数

adaline:cost=(errors ** 2).sum()/2.0  #平方误差的总和

logistic: cost=-y.dot(np.log(output)) -((1-y).dot(np.log(1-output)))

• 激活函数改成Signoid函数

adaline:
def activation(self,X):
return self.net_input(X)

logistic:
def activation(self,z)
return 1.0/(1.0+np.exp(-np.clip(z,-250,250)))

• 预测函数输出改为1,0

adaline:
def predict(self, X):
return np.where(self.activation(self.net_input(X)) >= 0.0, 1, -1)

logistic:
def predict(self, X):
return np.where(self.net_input(X)>0.0,1,0)

代码可以在这里看到。